This is the category of all types:

$$\begin{CD} Float @>toString>> String \\ @VfloorVV @VisEmptyVV \\ Int @>isOdd>> Bool \\ \end{CD}$$

Glossing over some mathematical details, a category is just a bunch of things, called objects, and arrows between them, called morphisms.

As far as category theory is concerned, the objects are shapeless blobs, they hold no structure or information other than the meaning we give them. Morphisms also are just arrows; they have a source and a target, but we know nothing else about them.

In the category of types, the arrows I drew between objects are regular functions; but morphisms can also look very different. in the category of dogs, where objects are dogs, we might have morphisms representing whether one dog has sniffed another.

$$\begin{CD} Fido @>>> Snuggles @>>> Waldo \\ \end{CD}$$

Also, I lied; the image at the top is not actually the category of types — it’s just a diagram in the category of types, meaning a small part of it. Drawing the whole thing would be impossible because there are infinitely many objects in it, with even infiniter morphisms.

Functors

One elementary concept in category theory is functors. A functor is like a function between categories: it maps objects to objects, and morphisms to morphisms, in a structure-preserving way.

For example, we can define a functor F from the category of types to the category of dogs. This functor maps every type to the dog Fido, and every function to the morphism that goes from Fido to Fido. (I haven’t drawn that earlier, but every object in a category has an identity morphism that goes from itself to itself.

I switch to figma for this because KaTeX can’t do nice diagrams and I’m too lazy to learn TikZ.

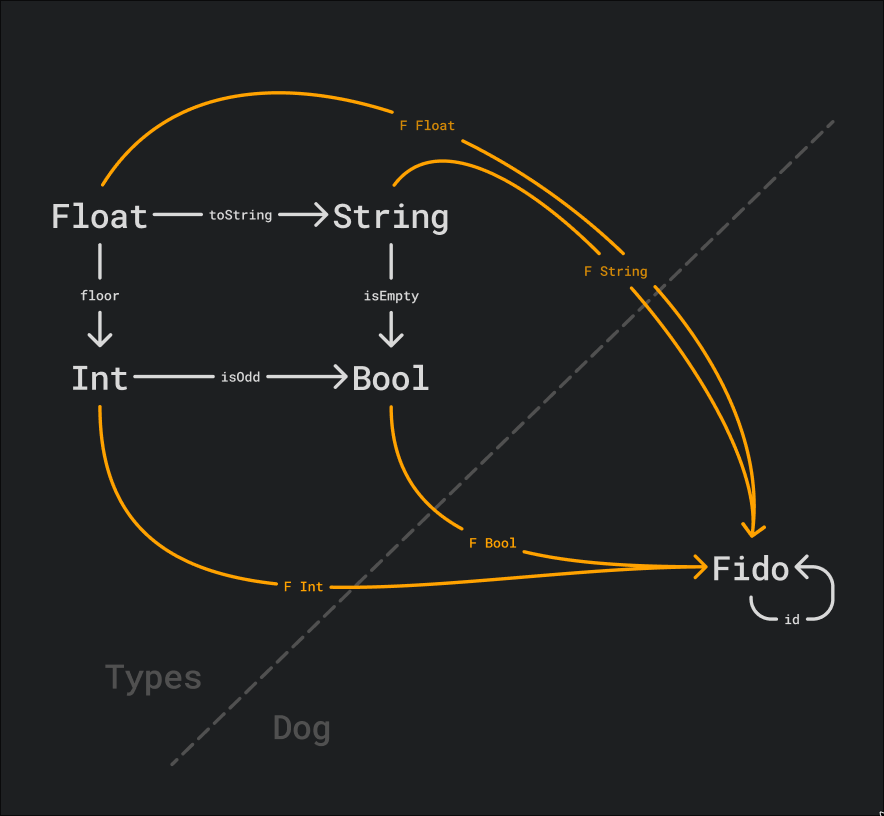
And, what’s not drawn in the image: $F(toString) = F(floor) = F(isEmpty) = F(isOdd) = id$

It also has to be noted that the orange arrows in the image are not morphisms in either category; they just represent the mapping that the functor performs.

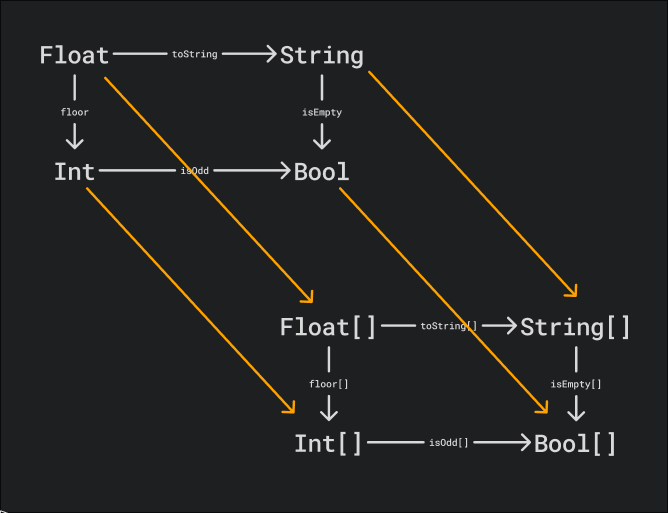
Perhaps a more useful functor, and one that is more well-known, is the List functor. This functor maps every type A to the type A[], and every function f: A -> B to the function f[]: A[] -> B[] that applies f to every element in the list, which in programming we would commonly call map(f).

That functor happens to be endo aswell because the source and target categories are the same.

Diagrams are just functors

We said that the category of types is too big to draw, as is the category of dogs, so we only draw small parts of them, called diagrams, yes?

Well, every diagram is just a functor. Recall this diagram in the category of dogs:

$$\begin{CD} Fido @>>> Snuggles @>>> Waldo \\ \end{CD}$$

We can represent it as a functor D from the category with three objects and two morphisms (let’s call this category 3) to the category of dogs. Let’s not even bother naming the objects in 3, these objects are just meaningless placeholders.

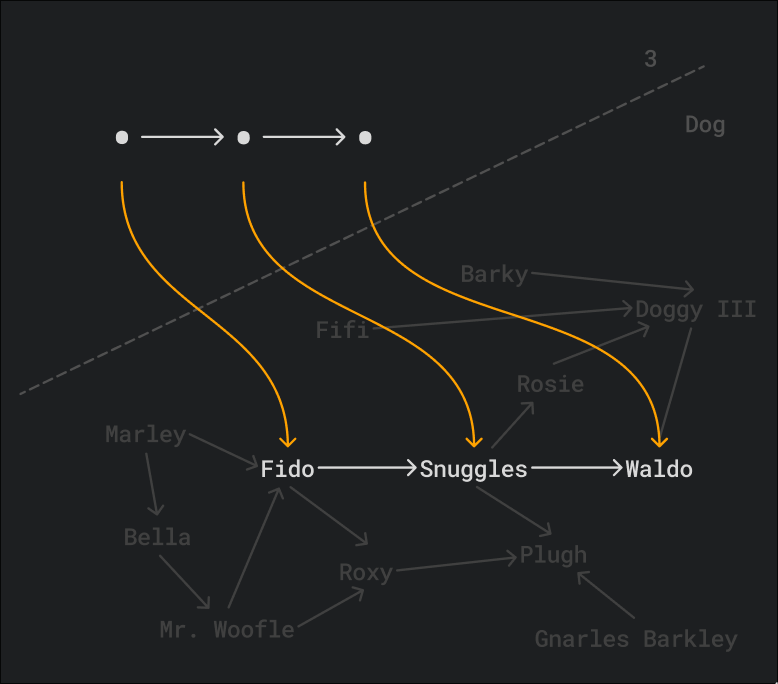
The source category of our functor acts as an “indexing category” that represent the shape and size of the diagram.

Diagrams are a category

Let’s consider all diagrams in the category of dogs. That is, given the very large category of all dogs, we consider all the pictures we can draw of it.

Let me give you two more examples: First, the diagram JustFido that goes from a category with one object to the category of dogs, mapping the single object to Fido. Or perhaps a functor E that is just our diagram D from earlier, but with Mr. Woofle added.

All these functors we can take and shove into a new category, called the diagram category of dogs $Diag(Dog)$.

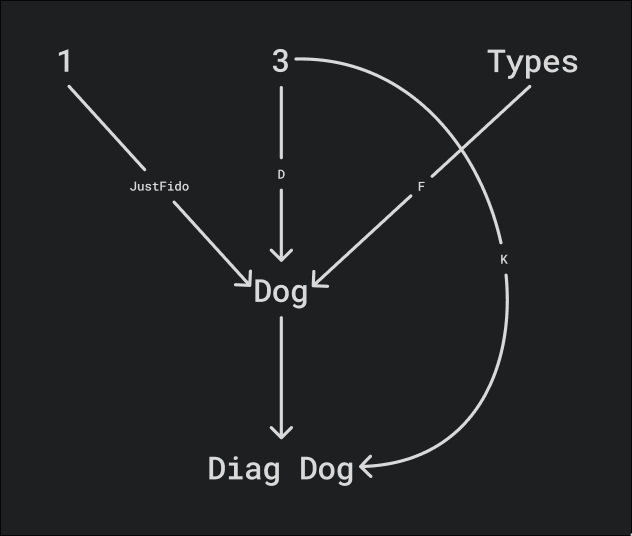
Here’s a diagram K of our diagram category:

$$\begin{CD} E @>>> D @>>> JustFido \\ \end{CD}$$

Of course that diagram is itself a functor from the category 3 to the diagram category of dogs $Diag(Dog)$ so if we were to draw the category $Diag(Diag(Dog))$ we could draw the diagram K in it.

Confused yet?

Well.

You might have seen that I have drawn arrows between the objects in this diagram above, and wonder what they represent. They’re actually functors aswell, but let’s not go overboard.

Categories are a category

There’s quite a lot of categories around. In this post alone we’ve looked at the category of types, the category of dogs, the category with three objects, the category with one object, the diagram category of dogs, and the diagram category of the diagram category of dogs,

Perhaps we should draw a diagram of all these categories to keep track.

The category of all (small) categories, $Cat$, has all our categories and more as objects, and the morphisms between them are functors.

It’s interesting how on the one hand our functor D is an arrow in $Cat$, but it is also object in $Diag(Dog)$. But category theory is funny like that, everything can be defined in terms of everything else.. that’s why it is sometimes called the “primordial soup” of maths. And even though I’m far from an expert, the more I look at categories, the more I can appreciate how “mathematical structure” is just an emergent property arising from relationships between objects.

Like, when I write $Int$ into a diagram, I’m putting images into your head of the set of integers {0, 1, 2, …} and perhaps addition or whatever else you can do with them. But really, $Int$ is just a dot I gave a label to; the dot looks like any other dot in the diagram. However, by looking at the right categories in the right ways, you can recover any information about integers you want — everything is encoded somewhere.